初中数学是每个学生必须掌握的一门重要学科,而公式是数学中的关键工具。掌握这些公式,不仅能帮助你更好地解决数学问题,还能为以后的学习打下坚实的基础。本文将详细介绍初中数学中的各种公式及其应用方法。
初中数学基础公式
初中数学的基础公式主要包括基本的代数公式、几何公式和比例公式等。这些基本公式是解决复杂数学问题的基础。
代数公式是初中数学的重要组成部分。例子包括平方公式:\( (a + b)^2 = a^2 + 2ab + b^2 \) 和立方公式:\( (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 \)。这些公式常用于多项式的展开和化简。
几何公式同样是初中数学中不可或缺的部分。包括三角形的面积公式:\( S = \frac{1}{2}ah \),其中 a 是底边长,h 是高;圆的面积公式:\( S = \pi r^2 \),其中 r 是圆的半径;以及圆的周长公式:\( C = 2\pi r \)。
比例公式在处理相似形等问题时也非常重要,比例中项公式:如果 \( \frac{a}{b} = \frac{c}{d} \),那么 \( a \times d = b \times c \)。这些公式能够帮助学生解决涉及比例和比例关系的问题。
统计与概率公式
统计与概率是初中数学的另一个重要领域,其中涉及许多关键的公式和概念。在统计部分,学生需要掌握平均数、众数、中位数等计算公式。平均数公式:\( \text{平均数} = \frac{\sum x}{n} \),其中 \( \sum x \) 是所有观测值的总和,n 是观测值的数量。
众数是指数据集中出现频率最高的数值,而中位数则是将所有数据从小到大排列后处于中间位置的数值。在概率部分,基本公式包括:概率 = \( \frac{\text{有利事件的数目}}{\text{总事件的数目}} \)。
组合与排列也在概率计算中占有重要地位。组合公式:\( C(n, k) = \frac{n!}{k!(n-k)!} \),排列公式:\( P(n, k) = \frac{n!}{(n-k)!} \),这些公式用于计算某些事件的发生次数和排列方式。
函数与方程公式
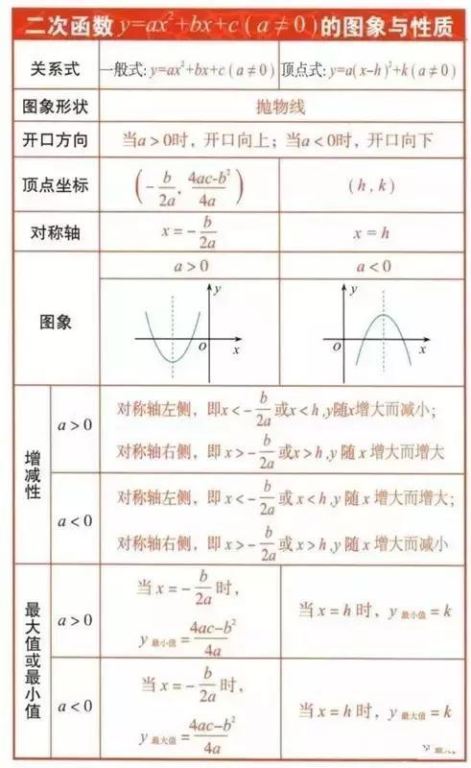
函数与方程在初中数学中扮演着至关重要的角色。常见的函数包括一次函数、二次函数等。一元一次函数的标准形式为 \( y = mx + c \),其中 m 为斜率,c 为截距。一元二次函数的标准形式为 \( y = ax^2 + bx + c \),其中 a, b, c 为常数。
解方程也是数学中的重点,常见的方程有一次方程、二次方程及其解法。一次方程的解法通常很简单,二次方程的解法则包括求根公式法:解 \( ax^2 + bx + c = 0 \) 的求根公式为 \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)。
学生还需要掌握因式分解法,通过将多项式分解成数项连乘的形式来解方程。,\( a^2 - b^2 = (a - b)(a + b) \) 和 \( a^3 \pm b^3 = (a \pm b)(a^2 \mp ab + b^2) \)。
Q&A
Q: 初中数学中常用的代数公式有哪些?
A: 常用的代数公式包括平方公式 \( (a + b)^2 = a^2 + 2ab + b^2 \) 和立方公式 \( (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 \)。
Q: 统计中的平均数公式是什么?
A: 平均数公式为 \( \text{平均数} = \frac{\sum x}{n} \),其中 \( \sum x \) 是所有观测值的总和,n 是观测值的数量。
Q: 一次函数的标准形式是什么?
A: 一次函数的标准形式为 \( y = mx + c \),其中 m 为斜率,c 为截距。
Q: 二次方程的求根公式是什么?
A: 二次方程 \( ax^2 + bx + c = 0 \) 的求根公式为 \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)。
Q: 什么是因式分解法?
A: 因式分解法是将多项式分解成数项连乘的形式, \( a^2 - b^2 = (a - b)(a + b) \)。









