初中数学是学生在学习阶段的一个重要部分,而掌握数学解题模型可以帮助学生迅速提高成绩。这篇文章将详细介绍初中数学48个解题模型,并探讨如何有效利用这些模型来解决数学难题。通过本文,学生和家长将能了解到关键的技巧和模型解析,进一步增强数学学习的效果。
常见数学解题模型简介
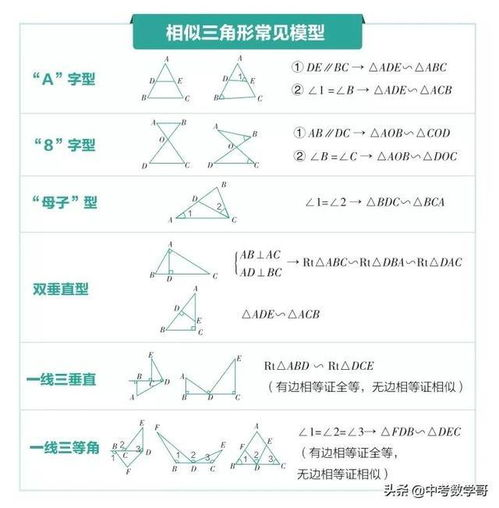
在初中数学学习过程中,有一些常见的解题模型是绝大多数题目都会涉及的。掌握这些模型,可以帮助学生在考试中更好地分配时间、提高正确率。
代数模型是初中数学中的基础模型之一。许多数学问题都可以通过代数方法来解决,包括代数方程和不等式。,设定变量、列方程求解是解决很多代数问题的基础。
几何模型也是初中数学的重要部分。几何问题通常包括三角形、四边形、圆的性质以及面积和周长的计算,学生需要熟悉各种几何定理,如勾股定理、相似三角形等。
第三,数论模型涉及整数的性质和运算。在初中,常见的数论问题有质因数分解、最大公约数和最小公倍数的求解等。通过这些基本的数学模型,学生可以快速解决许多数论问题。
典型解题模型的详细解析
为了更好地理解和应用初中数学48个解题模型,我们需要对部分典型解题模型进行详细解析。
其一,设椭圆问题,这是一个重要的几何问题。在解决这类问题时,我们需要应用到椭圆的定义、焦点性质和轨迹方程。,给定椭圆的长短轴,可以通过公式直接求解轨迹方程,从而解决问题。
另一个典型模型是求解函数问题。在初中数学中,函数问题经常出现,如一次函数和二次函数。学生需要熟练掌握函数的定义域、值域以及图形特征。,通过研究函数的变化趋势和极值位置,可以解决一些复杂的函数问题。
我们还需要了解概率统计模型。初中数学中的概率问题包括事件的可能性、概率计算等,而统计问题则涉及到数据的收集和分析。掌握这些模型有助于解决数据处理和预测问题。
提高解题技巧的实战策略
掌握了解题模型之后,如何提高解题技巧呢?以下几种策略可以帮助学生在实战中更好地应用这些模型。
要多加练习。解题模型的掌握需要通过大量的题目练习来实现。学生可以通过做题提高对模型的理解,并通过反复练习来巩固。
学习。每次做完题目后,学生应解题过程,分析解题思路,找到解决问题的关键点,并记住这一过程,下一次遇到类似题型时就能迅速找到解决方法。
再者,注意错题整理。错题是数学学习中的重要资源。整理错题并认真分析错误原因,可以避免以后再犯同样的错误,从而提高解题的准确率。
提高阅读理解能力。许多数学题目是文字题,学生需要具备良好的阅读理解能力,快速抓住问题的关键信息。通过多读、多练,提升理解文字题目的能力。
与常见问题解答
掌握初中数学48个解题模型是提高数学成绩的关键。学生需要通过多练习、学习、整理错题和提高阅读理解能力,才能更好地应用这些模型。以下是一些常见问题及其解答,供大家参考。
常见问题解答
问题1:初中数学解题模型有哪些实用技巧?
答:实用技巧包括代数模型的应用、几何模型的运用和数论模型的实践。结合大量练习和错题,可以更好地掌握这些技巧。
问题2:如何提高解题速度?
答:通过多做题、多经验、整理错题和增强阅读理解能力,可以有效提高解题速度。
问题3:如何处理难题?
答:遇到难题时,冷静分析,找出问题的关键信息,尝试将其分解为几个小问题逐一解决。如果仍然无法解决,可以请教老师或同学。
问题4:如何在考试中高效使用解题模型?
答:考试中,先做自己有把握的题目,节省时间,再通过解题模型的方法逐一解决较难的题目,确保时间分配合理。









